| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 교환학생
- 미래에셋해외교환
- fluent python
- 특별 메소드
- 미래에셋 장학생
- m1 anaconda 설치
- 청춘 화이팅
- Deeplearning
- 최소공배수
- 2022년
- Machine learning
- 최대공약수
- 오스트리아
- special method
- 이차전지
- Python
- Linear Regression
- 유럽 교환학생
- gradient descent
- 나의23살
- set add
- 최소제곱법
- 유럽
- cost function
- Andrew ng
- 딥러닝
- anaconda 가상환경
- 선형회귀
- 양극재
- set method
- Today
- Total
Done is Better Than Perfect
02. Linear regression with one variable 본문
이번에는 앞서 공부했던 Supervised Learning에서 regression을 더 자세히 살펴볼 것이다.
집 값을 예측하는 Linear Regression을 학습하며 cost function과 gradient descent의 개념도 함께 알아보자.
1. Linear Regression Model
변수가 1개인 linear regression을 univariate linear regression이라 표현한다.

저번에 예시로 학습했던 'Housing Price' 예제에서 사이즈(x)에 따른 집의 가격(y)을 예측할 수 있었다.
위의 그래프에서는 집의 사이즈가 커지면 가격이 높아지는 일차 방정식으로 표현하였다.
** 여기서 직선은 input(feature)와 output(target)의 관계를 나타내는 함수이다.
이 개념을 아래와 같이 도식화해보도록 하자.

위 그림에서 h는 직선 함수를 의미하고, 가설함수(hypothesis function)라 부른다. 가설함수(h함수)를 이용하여 데이터(x)를 입력하면 그에 상응하는 예측 결과(y)를 얻을 수 있다.
머신러닝은 우리가 알고자 하는 가설 함수(h 함수)를 찾아준다.
training set이 학습 알고리즘을 거쳐 h 함수(hypothesis function, 가설함수)를 생성한다.
2. Cost Funtion
(cost function = squared error function = mean squared error)
한 줄 요약 : cost function은 가설 함수(h)에서 최적의 parameter θ 를 찾는 도구이다.
우리가 가설함수를 잘 설정했다고 어떻게 알 수 있을까?
가설함수를 이용해 구한 예측값과 실제값이 차이가 작을수록 좋은 가설함수라 말할 수 있다. [이해 참고, MSE]
(여기서 예측값과 실제값이 차이를 cost라 한다.)
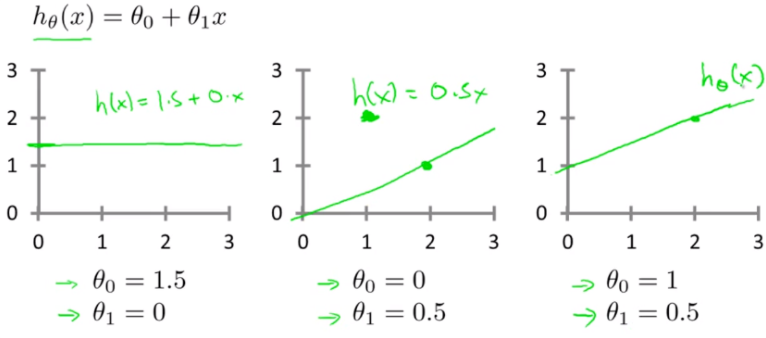
이전에 구한 일차방정식의 가설함수를 $h_{\theta}(x) = \theta_{0} + \theta_{1}x$ 라 하자.
여기서 $\theta_{0}, \theta_{1} $를 parameter라 한다.
cost는 '예측값(h) - 실제값(y)'로 정의한다. 이 값이 (-) 값을 가질 수 있으므로 제곱을 적용한다. 이를 수식으로 표현하면 다음과 같다.

(m은 training set의 개수이다.) 모든 cost 값을 제곱하고 $2m$을 나누어 평균값을 구한다. 위의 식이 cost function이다.
이 cost function $J(\theta_{0}, \theta_{1})$의 값을 최소화하는 parameter $\theta_{0}, \theta_{1}$을 구하는 것이 목표이다.

$h_{\theta}(x) = \theta_{0} + \theta_{1}x$에서 $\theta_{0} = 0$ 이라 가정하고 $ \theta_{1}$에 여러 값을 대입해보자.
아래 오른쪽 그림은 각 $\theta_{1}$의 값에 따른 cost function의 값을 의미한다. $ \theta_{1} = 1$ 일때 cost function($J$)가 최소값을 갖는 것을 알 수 있다.
이 의미는 $ \theta_{1} = 1$일때 가설 함수가 데이터에 가장 잘 적합 되었다는 것을 의미한다.

이제 1개의 parameter에서 2개의 parameter로 확장해보자.
2개의 parameter($\theta_{0}, \theta_{1} $)에 대하여 cost function($J$)을 그리면 아래와 같이 3차원으로 표현된다.

여기서 cost function($J$)이 가장 작은 값을 가질 때, parameter $\theta_{0}, \theta_{1}$이 적합하다는 것을 알 수 있다.
이제 $J$가 최소화 되도록 $\theta_{0}, \theta_{1}$을 자동으로 찾는 알고리즘을 알아보도록 하자.
3. Gradient Descent
앞에서 가설함수(hypothesis function)에 대해 알아보았고, 실제 training data에 얼마나 잘 적합하는 지 알아보기 위해 cost function을 학습하였다. cost function을 통해 $\theta$의 값에 따라 가설함수(h)의 정확도를 측정할 수 있었다. 하지만, 어떻게 적절한 $\theta$값을 찾는지 알 수 없었다. 이번에는 가장 적합한 가설함수(h)를 특정하기 위한 $\theta$를 찾는 알고리즘을 알아보도록 한다.
한 줄 요약 : Gradient Descent는 가장 적합한 가설 함수를 찾는 알고리즘이다.
(더 정확하게 말하자면 cost function을 최소화하는 $\theta$ parameter를 찾는 알고리즘)
Gradient descent algorithm은 말 그대로 경사면을 따라 하강하는 알고리즘이다.
두 개의 parameter($\theta_{0}, \theta_{1})을 변경하여 cost function을 최소화(minimize)한다.
아래의 그래프는 2개의 feature를 가진 cost function의 그래프이다.
시작점을 왼쪽의 봉우리로 잡는다면 경사면을 따라 아래와 같은 최저점에 도달할 것이다.

만약 시작 점을 다른 곳에서 시작했을 경우, 위와 다른 경로의 최저점에 도달한다. 이렇게 나온 최저점은 local minimum이라 한다.
최적 parameter를 얻기 위해서는 local minimum 들 중에서도 가장 작은 global minimum을 구해야 한다.

최적 cost function을 구하기 위한 gradient descent의 수식은 다음과 같다. 이 수식은 한 점에 수렴할 때 까지 반복된다.
수식에서 $\alpha $는 'learning rate'라 한다. 간단히 설명하자면 step(보폭)이라 이해하면 된다.
보폭이 큰 사람일수록 한 번에 걷는 길이가 크고, 보폭이 작은 사람은 총총걸음으로 걷는 원리와 비슷하다.
그리고 두 개의 파라미터 $\theta_{0}$와 $\theta_{1}$는 동시에 업데이트되므로 simultaneous update라 한다.
(실제로는 $\theta_{0}, \theta_{1}$뿐만아니라 $ ~ \theta_{n}$ 까지 있다.)

수식을 하나씩 뜯어보도록 하자. 수식에서 미분은 왜 있는 걸까?
우선 수식을 이해하기 위해 $\theta_{1}$만 살펴 보면,
만약 현재 $\theta_{1}$ 값이 최저점보다 큰 경우, 위쪽 그래프와 같이 표현된다. 여기서 J함수를 미분(기울기)하면, 양수 값을 가지게 된다. 이를 gradient 공식에 넣으면 현재 $\theta_{1}$ 값보다 작은 값을 얻을 수 있다. (경사를 따라 내려감)
다음으로, 만약 현재 $\theta_{1}$ 값이 최저점보다 작은 경우, 아래쪽 그래프와 같이 표현된다. J함수를 미분(기울기)하면, 음수 값을 가지게 된다. 이를 gradient 공식에 넣으면 현재 $\theta_{1}$ 값보다 큰 값을 얻을 수 있다. (경사를 따라 내려감)
이와 같이 미분을 통해 최저점을 향해 수렴(이동)할 수 있다.


다음은 learning rate 인 $\alpha$에 대해 알아보자. 앞에서 $\alpha$를 step으로 비유하였다.
만약 $\alpha$가 너무 작으면 아래 그림의 위쪽 그래프과 같이 최저점을 찾는데 많은 단계와 많은 시간이 걸린다. 교수님은 이를 'baby step downhill'이라 표현했다.
반면 $\alpha$가 너무 크면, 최저점보다 over하여 위치를 잡다가 잘못 꼬여 최저점으로 수렴(converge)하지 못하고 거꾸로 발산(diverge)하는 경우도 있다.

또한, 우리가 최저점에 가까워질수록, gradient descent 수식도 자연스럽게 step이 작아진다.(기울기가 작아지기 때문에)
그래서 $\alpha$ 값을 추가적으로 조정할 필요가 없다.
이제 각 parameter의 gradient descent식을 하나씩 살펴보자.

우리가 배운 gradient descent는 두 개의 parameter로 구성되어 있고, 이를 각각의 parameter로 편미분하면 아래와 같이 두개의 식 만들어진다. 편미분을 하면 제곱($^2$)이 $\frac{1}{2}$로 내려오므로 $\frac{1}{m}$으로 나눠진다.
$\theta_{0}$는 원래 상수(costant)이므로 x(input data)가 사라지고, $\theta_{0}$식으로 미분한 것은 x(input data)가 곱해진다.


이제 cost function에 대한 gradient descent를 배웠다. 이와 같이 최저점을 찾을 때까지 반복적으로 움직이는 알고리즘은 'batch gradient descent'라 한다.
grdient descent는 local minimum에 영향을 받지만, 이 문제를 해결하기 위해 위의 그림처럼 생긴 cost function을 하나의 global minimum을 갖는 그래프 형식(볼록한 2차 함수)으로 바꾼다.


따라서 learning rate $\alpha$가 너무 크지 않다고 가정할 때, gradient descent는 항상 global minimum 값으로 수렴된다.
_______참고 자료_______
'공부 > MachineLearning' 카테고리의 다른 글
| 04. Logistic Regression (0) | 2022.03.23 |
|---|---|
| 03. Linear Regression with Multiple Variable (0) | 2022.02.10 |
| 01. introduction (0) | 2022.01.20 |
| Machine Learning 정리 (0) | 2022.01.20 |
| 추천 시스템이란 (0) | 2022.01.05 |


