| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 2022년
- gradient descent
- 유럽
- 오스트리아
- 선형회귀
- 이차전지
- special method
- Deeplearning
- 딥러닝
- fatigue fracture
- 미래에셋 장학생
- Python
- 교환학생
- electrochemical models
- Linear Regression
- 나의23살
- li-ion
- 청춘 화이팅
- set method
- Machine learning
- Andrew ng
- 미래에셋해외교환
- cost function
- 유럽 교환학생
- set add
- anaconda 가상환경
- 특별 메소드
- fluent python
- m1 anaconda 설치
- 양극재
- Today
- Total
Done is Better Than Perfect
04. Logistic Regression 본문
목차
1. Classification
classification은 데이터의 결과를 0또는 1로 분류하는 모델이다. 예를 들어, 메일의 스팸여부와 암의 악성 여부를 판단할 때 사용된다.
일반적으로 참, 거짓으로 분류되는 모델에서 1을 positive class, 0을 negative class로 표현한다.
추후에 2개 이상의 카테고리로 분류하는 multiple-class classification도 학습할 것이다.

Linear regression을 classification에 적용하면 위의 그림과 같이 오른쪽에 동떨어진 데이터가 추가될 경우 h함수(가설함수)가 바뀌기 때문에 판단을 잘못하는 결과를 야기한다. 따라서, classification에 linear regression을 사용할 수 없다.
2. Hypothesis Representation
h함수(가설함수)의 값이 0 과 1사이의 값을 갖도록 Logistic Regression을 사용한다.
0≤hθ(x)≤1를 만족하시키기 위해서 가설함수 hθ(x)를 g(z)의 형태로 변환한다.
이 g함수는 아래와 같은 공식으로 나타내며 이를 sigmoid function 또는 Logistic function이라 한다. 이 함수를 그래프로 표현하면 아래와 같이 완만한 S자 형태를 띤다.
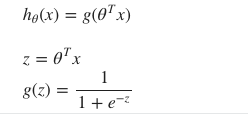

hypothesis(h함수)의 결과는 x가 결정되었을 때, y가 1이 되는 확률을 의미한다.
만약 h 함수의 값이 0.7로 나왔다면, 이것은 최종 결과(y)가 1일 가능성이 70%다 라고 말할 수 있다.
h함수는 y = 1이 될 가능성이 x와 theta에 의해 결정된다.
반대로 y = 0이 될 가능성은 1 - (y가 1이 될 가능성)이다.

3. Decision Boundary
y가 0인지 1인지 판단하는 경계선을 decision boundary라 하고, 이는 가설 함수에 의해 결정 된다.
y가 1이 되는 기준을 살펴보면 h 함수가 0.5보다 큰 값이 되어야 하고 그와 동시에 theta transpose * x의 값이 0보다 큰 값이 되는 것과 동일합니다. 반대로 y가 0이 되는 기준을 보면 h 함수가 0.5보다 작은 값이 되어야 하며 동시에 theta transpose * x의 값이 0보다 작으면 y가 0이 됨을 알수 있습니다.
가령 hθ(x)≥0.5hθ(x)≥0.5 일때 y = 1이라고 가정한다면, hθ(x)=g(θTx)≥0.5hθ(x)=g(θTx)≥0.5 와 같다. 그래프를 보면 z≥0z≥0일때 g(z)≥0.5g(z)≥0.5이므로 z=θTx≥0z=θTx≥0 일때 와 같다.
즉 θTx≥0 이면, y=1 로 예측할 수 있다.
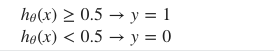
아래의 데이터에서 임의로 최적 parameter θ를 [-3,1,1]로 설정했다면. 이 최적 parameter를 가지고 다음과 같은 결론을 내릴 수 있다.
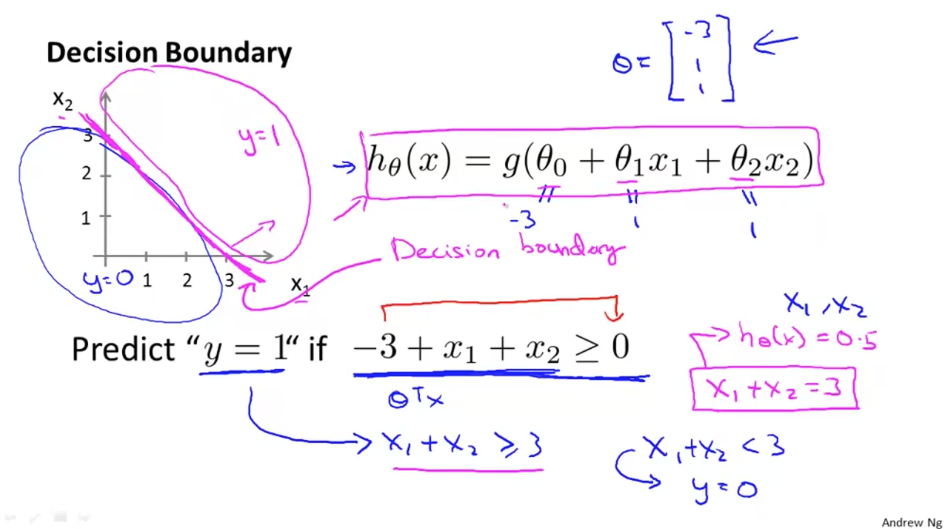

이 때의 decision boundary는 −3+x1+x2=0 이다. 위 그림에서 녹색으로 표시된 선이다. 이제 training set에 들어있지 않았던, 새로운 데이터가 나타나면 x1 값과 x2 값을 이용하여 좌표를 찍어보고, decision boundary보다 위쪽에 찍히면 class 1에, 아래쪽에 찍히면 class 0에 넣으면 되는 것이다.
이 때, decision boundary는 θ 에 의해 결정되는 것임을 기억하자. Training data는 parameter를 결정하는 데에 이용될 뿐, decision boundary 에 직접적으로 영향을 미치지는 않는다.
Non-Linear Decision Boundary
아래의 그림과 같이 decision boundary가 직선으로 주어지지 않는 경우가 있다.

이 경우 polynomial 하게 feature의 차원을 높여 non-linear decision boundary를 표현할 수 있다.
4. Cost Function
적절한 parameter θ를 구하는 방법은 cost function을 활용하면 된다.
이전에 Linear regresssion에서 사용했던 cost function과 다른 cost function 사용해야 한다.
Logistic function은 결과가 linear이 아니므로 많은 local optima를 생성하기 때문이다. (convex function X)
Logistic regression의 cost function은 다음과 같다.
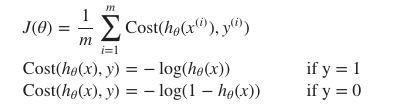
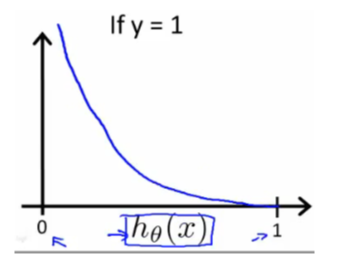
그래프를 자세히 풀어보자면,
y=1일 때, h함수(가설 함수)의 예측값이 1이 나와야하므로
이때 cost는 0이 되고,
y=1일 때, h함수(가설 함수)의 예측값이 0에 가까울수록 cost는 무한대로 증가하여 cost를 최소화하는 cost 함수를 확인하였다.
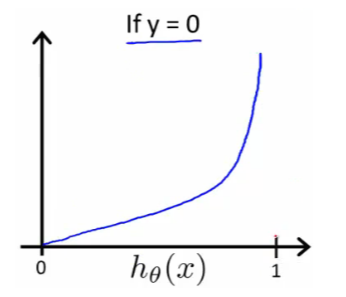
y=0일 때, h함수(가설 함수)의 예측값이 0이 나와야하므로
이때 cost는 0이 되고,
y=1일 때, h함수(가설 함수)의 예측값이 1에 가까울수록 cost는 무한대로 증가하여 cost함수에 적합하다는 것을 확인할 수 있다.

Simplified Cost Function
y = 0또는 1의 값만 가지기 때문에 다음과 같이 하나의 식으로 간단히 표현 가능하다.

전체 cost function( J(θ))을 표현하면 다음과 같다.
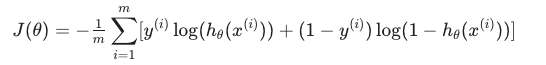
vector형태로 식을 표현하면 다음과 같다
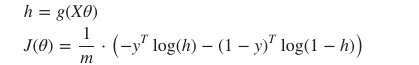
Gradient Descent
cost가 가장 작은 경우의 parameter θ를 찾기 위해 gradient descent를 적용한다.
이때, 각 θ 값은 동시에 계산(업데이트)된다.
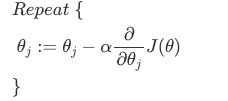
편미분하고, 도함수(Derivative)를 대입하면 다음과 같다.
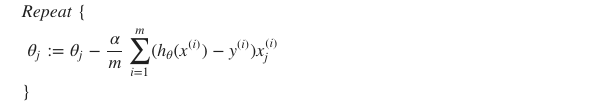
주의 ! ) 여기서 linear regression의 gradient descent와 형태는 같지만 h 함수가 다르다.
- Linear regression
- Logistic regression
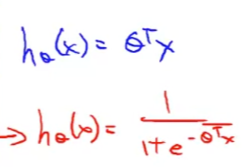
vector 형식으로 표현하면 다음과 같다.

5. Advanced Optimization
앞에서 cost가 가장 작은 경우의 parameter θ를 찾기 위해 gradient descent를 알아보았다.
gradient descent 외에 다른 optimization algorithm도 있다.
- Conjugate gradient
- BFGS (Broyden-Fletcher-Goldfarb-Shanno)
- L-BFGS (Limited memory - BFGS)
이 알고리즘은 gradient descent 보다 더 빠르고, learning rate(알파)를 선택하지 않아도 된다는 장점이 있지만,
더 복잡한 알고리즘이라는 단점도 있다.
6. Multiclass Classification
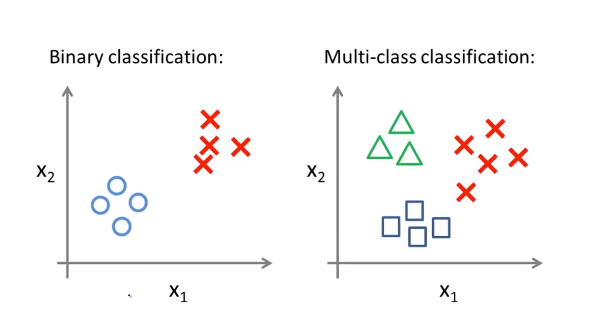
앞에서는 y가 0또는 1의 결과값만을 가지는 binary classification을 알아보았다.
이제는 그 개념을 확장하여 2개 이상의 카테고리로 분류하는 multiclass classification에 대하여 알아보도록 하자.
multiclass classification의 예시
ex) email tagging, medical diagram, weather
y가 n개의 카테고리로 결과가 나올 때, n개의 binary classification 문제로 나누어 생각한다. (one VS all)
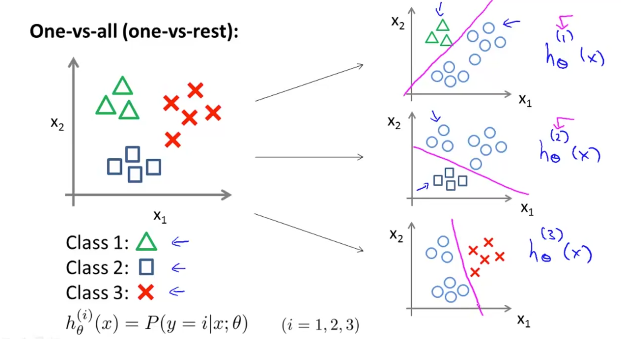
이 one VS all 방식을 정리하자면,
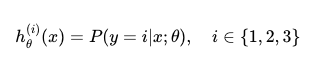

hypothesis function은 주어진 x가 class i 에 들어갈 가능성을 나타낸다.
즉, hypothesis function이 가장 큰 것은 해당 class에 속할 확률이 가장 크다는 의미이다.
😀 수정해야 할것 : 식을 전부 회색 사각형 안에 들어간 형식으로 바꾸기!!!!!
수식 정리!!!
'🤖 AI > Machine Learning' 카테고리의 다른 글
| 05. Regularization (0) | 2022.03.25 |
|---|---|
| 03. Linear Regression with Multiple Variable (1) | 2022.02.10 |
| 02. Linear regression with one variable (1) | 2022.02.04 |
| 01. introduction (0) | 2022.01.20 |
| Machine Learning 정리 (0) | 2022.01.20 |



