| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- electrochemical models
- 특별 메소드
- cost function
- 오스트리아
- fluent python
- fatigue fracture
- anaconda 가상환경
- Andrew ng
- Linear Regression
- set method
- Deeplearning
- 청춘 화이팅
- 선형회귀
- set add
- 나의23살
- gradient descent
- 유럽
- 미래에셋해외교환
- 딥러닝
- 이차전지
- Python
- Machine learning
- special method
- 유럽 교환학생
- 미래에셋 장학생
- li-ion
- 교환학생
- 2022년
- 양극재
- m1 anaconda 설치
- Today
- Total
Done is Better Than Perfect
05. Regularization 본문
목차
저번 포스트에서는 지도학습의 Linear Regression모델과 Logistic Regression 모델을 배웠다.
이번에는 h함수를 더 자세히 알아보도록 하자.😀
1. Overfitting Problem
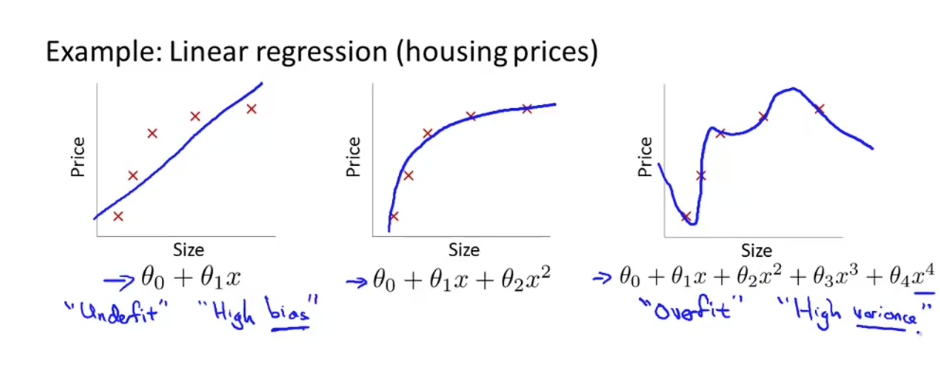
가장 왼쪽 그래프의 경우, h함수(가설 함수)를 θ에 대한 1차 방정식으로 정의 ➡ 데이터의 예측이 일치하지 않는다.
일반적으로 너무 단순하거나 너무 적은 기능을 사용하는 기능 때문에 발생한다.
이러한 경우를 Underfit 또는 High Bias라 한다.
가장 오른쪽 그래프의 경우, h함수를 다차원방정식으로 정의 ➡ 각각의 데이터 결과 값을 만족하는 형태를 띈다고 할 수 있다.
training data set에서는 최적화가 잘 되었다고 생각할 수 있지만 새로운 data에 대한 정확도는 장담할 수 없다.
즉, 너무 샘플데이터에 과하게 최적화되어있어 일반화하기 어렵다고 할 수 있다.
이러한 경우를 Overfit 또는 High variance라 한다.
이제 가운데 그래프를 보도록 하자.
h 함수를 2차 방정식으로 정의하여 dataset에 적합하면서 feature간의 관계를 잘 나타내고 있다.
이러한 경우를 Just Right라고 하며, 최적화가 적절히 되었다고 할 수 있다.
이제 Logistic Regression의 예를 보도록 하자.
Linear Regression의 overfitting을 이해했다면 똑같은 로직으로 이해가 가능하다.

더 많은 feature를 삽입 할수록, training data set에 잘 fit 이 된다.
하지만 새로운 데이터가 입력되었을 때 회귀 또는 분류모델에서 오차가 발생할 가능성이 매우 크다.
이와 같이 training data에 지나치게 fit 되어 일반적인 추세를 표현하지 못하는 문제를 overfitting이라 한다.
여기, overfitting을 해결하기 위한 방법이 있다.
1. feature의 수 줄이기
- 중요한 feature만 남기기
- model selection algorithm(모델이 빼야 하는 feature 알려준다.)
2. regularization(정규화)
- 모든 feature는 유지하되, parameter θ의 규모(magnitude) 줄이기
2. Cost Function
정규화의 개념을 알기 위해서 cost function의 설명이 필요하다.

그림의 오른쪽 그래프는 Linear Regressino에서 과적합이 된 예시이다.
이때, θ3, θ4에 각각 1000을 곱한 cost function을 사용한다고 가정해보자. 이 cost function은 θ의 가장 작은 값을 구하기 때문에 parameter(θ3,θ4)의 값은 거의 0에 가까운 값이 될 것이다.
결국, h 함수에서 뒤에 2개 항이 0에 근접하므로 2차 방정식으로 생각할 수 있다.
n개의 parameters에서 일부 parameter를 (0에 근사한)작은 값으로 만들어 h 함수가 심플해지도록 한다.
이 방법을 overfitting을 적게 발생시킬 수 있는 정규화라고 한다.
3. Regularization
이를 공식으로 표현하면 cost function에 regulation식을 추가하여 J함수로 만들 수 있다.
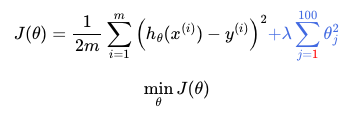
위의 식에서 λ(lambda)를 regularization parameter이라 한다. λ는 cost function가 잘 적용이 될수 있도록 조절한다.
** λ가 너무 큰 경우에는 θ의 parameter 값이 전부 0이 되어 underfitting하는 결과를 초래한다.
4. Regularized Linear Regression
이제 linear regression과 logistic regression에 regularize를 적용해보자.
Linear regression의 최적 θparameter를 찾는 방법은 gradient descent와 normal equation, 2가지 방법이 있다.
Gradient Descent
앞에서 cost function에 λ 항을 추가하여 정규화된 cost function을 만들었다. 이제 gradient descent 공식에 적용해 보자.
θ0는 정규화되지 않았으므로, 식을 분리하도록 주의해야 한다.
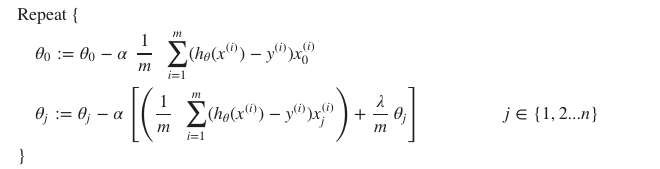
식을 하나로 표현하면 다음과 같다.
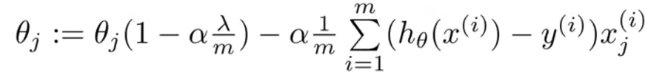
이 식에서 흥미로운 점은 항상 1−αλ/m<1이다. 그래서 θj가 update 할 때마다 줄어든다.
오른쪽 항은 기존의 linear regression의 gradient descent와 똑같다.
Normal Equation
X matrix는 m x (n+1)의 크기를 가진다. Normal equation에 regularize를 적용하려면 XTX항 뒤에 λL을 더한다.
이 때 L matrix는 첫번째 값만 0인 identity matrix이다. [차원은 (n+1) x (n+1)]
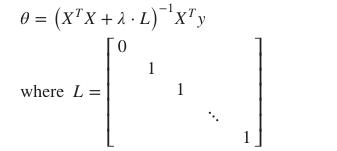
m < n이면, XTX는 non-invertible, singular이다.
하지만 정규화를 해주면, XTX+λ∗L은 invertible 해진다.
5. Regularized Logistic Regression
Logistic regression에서 regularize를 하는 방식을 알아보도록 하자.
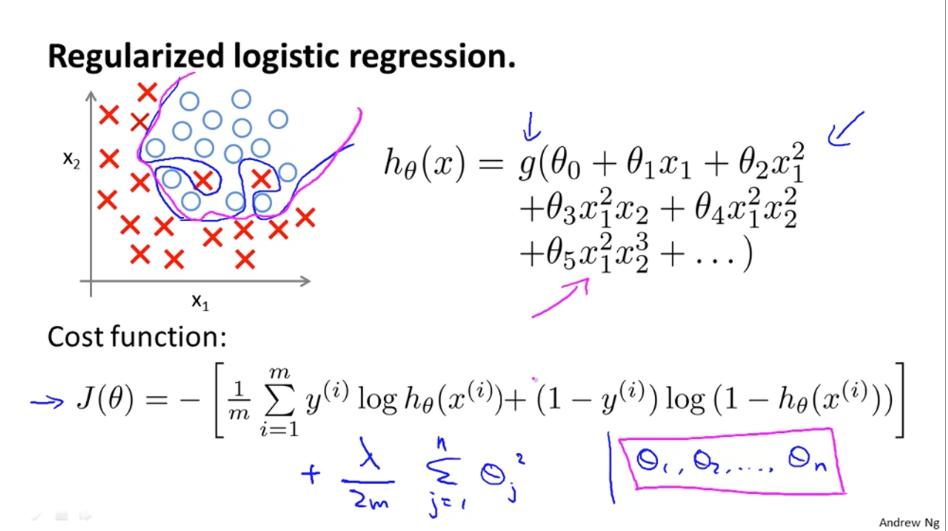
[위에 식도 내가 정리하기 ] https://wikidocs.net/4331 처럼 깔끔하게!!!
Regularized 된 cost function은 그림의 아래 J(θ) 과 같다. 기존 cost function에 λ 항이 추가되었다.
theta0를 정규화하지 않은 것에 주의해야 한다.
이를 gradient descent 에 적용하면,

마찬가지로 θ0는 정규화되지 않았으므로, 식을 분리한다.
이 공식은 regularized linear regression의 gradient descent와 식이 같지만 h 함수가 달라 다른 함수이다.
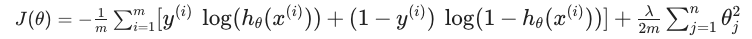
위의 식을 간단하게 정리하면 다음과 같다.
깔끔하게 식 정리!!1
+ 참고 자료
https://towardsdatascience.com/regularization-an-important-concept-in-machine-learning-5891628907ea
REGULARIZATION: An important concept in Machine Learning
Hello reader,
towardsdatascience.com
1) Cost Function
[TOC] # Intuition  이 때, θ3, $\the ...
wikidocs.net
'🤖 AI > Machine Learning' 카테고리의 다른 글
| 04. Logistic Regression (1) | 2022.03.23 |
|---|---|
| 03. Linear Regression with Multiple Variable (1) | 2022.02.10 |
| 02. Linear regression with one variable (1) | 2022.02.04 |
| 01. introduction (0) | 2022.01.20 |
| Machine Learning 정리 (0) | 2022.01.20 |




