| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- anaconda 가상환경
- 오스트리아
- Machine learning
- 나의23살
- 특별 메소드
- Linear Regression
- 2022년
- Python
- set add
- 이차전지
- 딥러닝
- 유럽
- 청춘 화이팅
- special method
- electrochemical models
- 양극재
- Andrew ng
- fatigue fracture
- Deeplearning
- gradient descent
- 미래에셋해외교환
- set method
- 교환학생
- 선형회귀
- 유럽 교환학생
- 미래에셋 장학생
- m1 anaconda 설치
- cost function
- fluent python
- li-ion
- Today
- Total
Done is Better Than Perfect
[딥러닝] 선형 회귀와 최소 제곱법 본문
딥러닝의 가장 말단에서 이루어지는 가장 기본적인 두가지 계산 원리가 있다.
1. 선형 회귀(linear regression) 2. 로지스틱 회귀(logistic regression)
오늘은 먼저 선형회귀를 알아보도록 하자!
선형 회귀 linear regression
선형회귀는 종속변수(y)와 한 개 이상의 독립 변수(x1, x2...)의 선형관계를 모델링 하는 회귀분석 기법이다.
독립 변수가 하나인 경우를 단순 선형회귀라 하고, 둘 이상인 경우 다중 선형회귀라 한다.
선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링한다. 알려지지 않은 파라미터는 데이터를 활용하여 예측한다.
이렇게 만들어진 회귀식을 선형 모델이라고 한다.
선형은 다음과 같은 일차함수의 형태를 띈다.
y = ax + b
선형 회귀의 목표는 알고 있는 데이터(x,y)로 알려지지 않은 데이터(a,b)를 예측하는 것이다.
기존 데이터를 기반으로 정확한 선을 그리기 위해서는 기울기 a와 y절편 b를 알아야 한다.
a,b 값을 얻기 위해 가장 많이 사용되는 방법은 최소제곱법이다.
최소 제곱법 method of least square
최소 제곱법은 어떤 계의 해방정식을 근사적으로 구하는 방법으로,
근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다.
최소 제곱법 공식을 알고 적용한다면, 이를 통해 일차 함수의 기울기 와 절편을 바로 구할 수 있다.
최소 제곱법은 x값이 하나일때 적용 가능하다.
x값이 여러개인 다중 선형회귀의 경우 경사하강법을 이용한다.
최소 제곱법은 임의의 선을 그리고 선을 평가하여 수정하는 방법 사용한다.
따라서, 주어진 선의 오차를 평가하는 오차평가 알고리즘이 필요하다.
이때, 주로 평균 제곱 오차(MSE, mean square error)를 사용한다.
기울기 a를 구하는 공식은 다음과 같다.
$$ a = \frac{\sum (x - mean(x))(y - mean(y))}{\sum (x - mean(x))^{2})} $$
y절편인 b를 구하는 공식은 다음과 같다.
$$ b = mean(y) - (mean(x)*a) $$
앞에 설명한 과정을 통해 일차함수 식 y = ax + b에서 a, b의 값을 얻을 수 있다.
일차함수 식에 새로운 x값을 넣으면 예측값인 y를 알 수 있다.
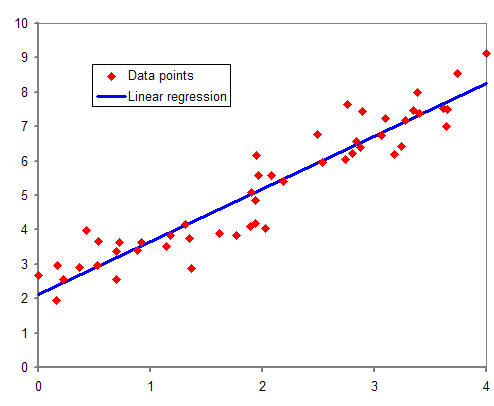
선형 회귀 - 위키백과, 우리 모두의 백과사전
독립변수 1개와 종속변수 1개를 가진 선형 회귀의 예 통계학에서, 선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모
ko.wikipedia.org
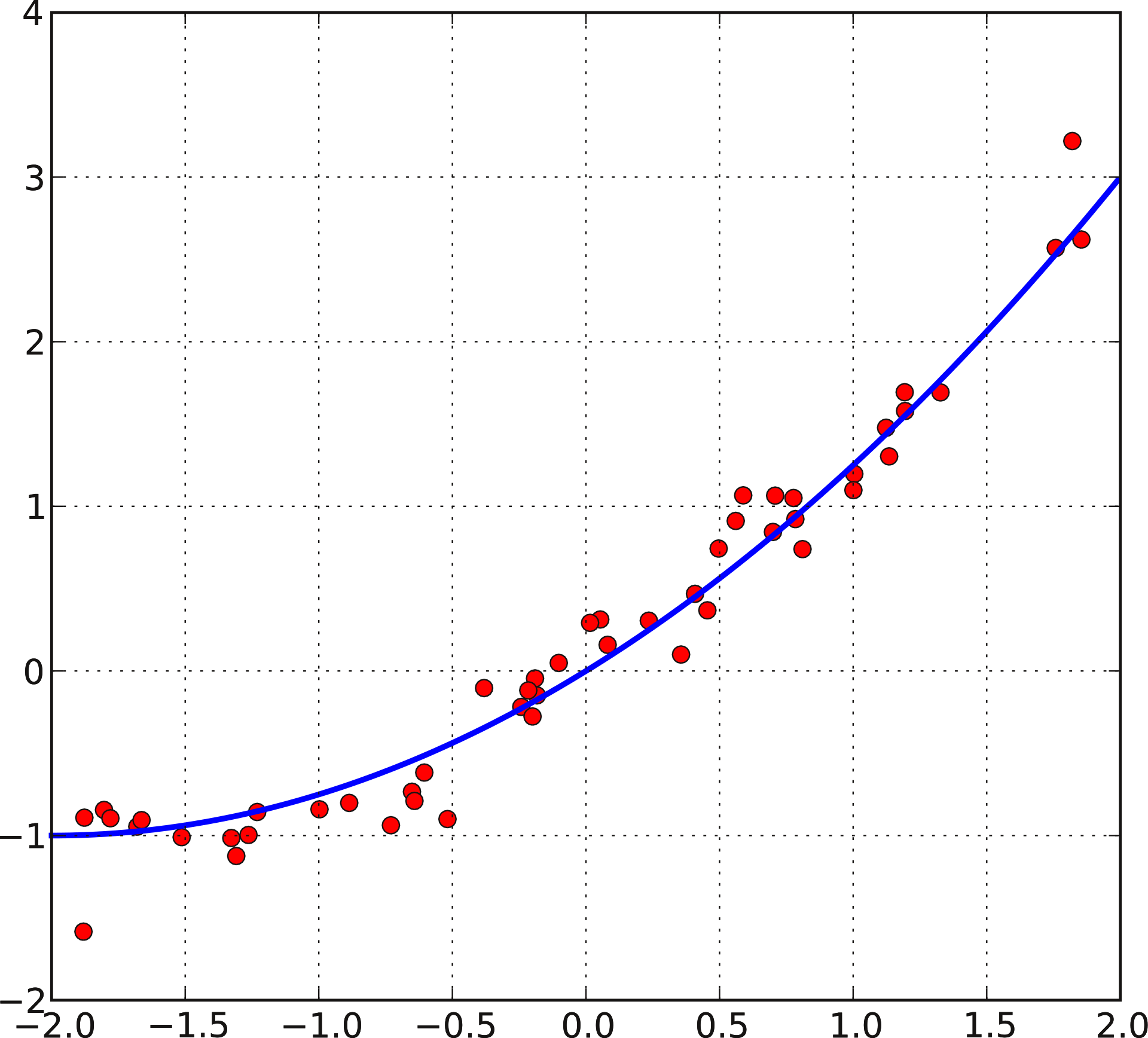
최소제곱법 - 위키백과, 우리 모두의 백과사전
붉은 점들을 기반으로 푸른 선의 2차 방정식 근사해를 구한다. 최소제곱법, 또는 최소자승법, 최소제곱근사법, 최소자승근사법(method of least squares, least squares approximation)은 어떤 계의 해방정식을
ko.wikipedia.org
* 이 글은 책 '모두의 딥 러닝'을 참고하였다.
'🤖 AI > 개발공부' 카테고리의 다른 글
| 🚙 H-모빌리티 클래스 (에너지 솔루션) 지원 과정 (1) | 2025.04.13 |
|---|---|
| [Fluent Python 스터디] Study Note #1 Data Model (1) | 2021.11.15 |
| [알고리즘] 최대 공약수, 최소 공배수 (1) | 2021.08.03 |
| [알고리즘] set method (0) | 2021.07.16 |
| conda 가상 환경 생성, 관리 (3) | 2021.07.14 |




