| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 양극재
- fluent python
- 특별 메소드
- anaconda 가상환경
- 이차전지
- set add
- Machine learning
- Linear Regression
- 나의23살
- 유럽 교환학생
- cost function
- 교환학생
- special method
- gradient descent
- 딥러닝
- electrochemical models
- li-ion
- Andrew ng
- 유럽
- set method
- m1 anaconda 설치
- Deeplearning
- 미래에셋해외교환
- fatigue fracture
- 2022년
- 미래에셋 장학생
- 오스트리아
- 선형회귀
- 청춘 화이팅
- Python
- Today
- Total
Done is Better Than Perfect
[딥러닝] 2. Backpropagation의 학습 본문
딥러닝 모델에서의 학습 : loss function을 최소화하기 위해 최적화 알고리즘 (gradient descent 등) 사용
- 딥러닝에서는 역전파(backpropagation)을 통해 각 가중치들의 기울기를 구할 수 있음
- backpropagation 정의 : 목표 target 값과 실제 모델이 예측한 output 값이 얼마나 차이나는지 구한 후, 오차 값을 다시 뒤로 전파해가며 변수들을 갱신하는 알고리즘
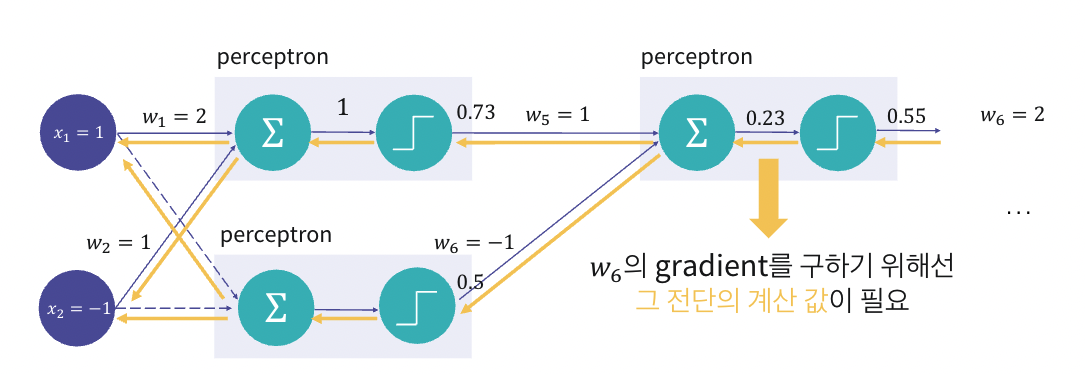
1. Backpropagation의 학습 단계
backpropataion은 체인 룰(chain rule)을 사용하여 손실 함수의 기울기를 계산하고, 이를 통해 가중치를 업데이트
1. Forward Propagation
- 입력 데이터가 신경망을 통과하면서 각 층에서의 출력 계산
- 각 뉴런의 출력은 다음과 같이 계산됨 :
$$ z=W⋅x+b $$
$$ a=σ(z) $$
여기서 $ W $는 가중치, $ x $는 입력, $ b $는 바이어스, $ \sigma $는 활성화 함수.
2. Loss Calculation (손실 함수 계산)
- 출력층에서 나온 예측값과 실제 레이블을 비교하여 손실 함수 계산
- 예를 들어, 평균 제곱 오차(MSE)의 경우 :
$$ L=\frac{1}{n}(y−\hat{y})^2 $$
여기서 $ y $는 실제값, $ \hat{y} $는 예측값.
3. 출력층에서의 기울기 계산
- 손실 함수 $ L $에 대한 출력층의 가중치 $ W $의 기울기 계산
- 출력층의 활성화 함수가 $ \sigma $일 때, 출력층의 손실 함수에 대한 기울기는 다음과 같이 계산:
$$ \frac{\partial L}{\partial \hat{y}} = \hat{y} - y $$
$$ \frac{\partial \hat{y}}{\partial z} = \sigma'(z) $$
$$ \frac{\partial z}{\partial W} = a_{\text{previous}} $$
여기서 $ a_{\text{previous}} $는 이전 층의 활성화 값.
4. 역전파(Backpropagation) 단계
- 출력층에서 계산된 기울기를 이전 층으로 전파
- 체인 룰을 사용하여 이전 층의 가중치에 대한 기울기를 계산함:
$$ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z} \cdot \frac{\partial z}{\partial W} $$
- 이를 반복하여 각 층의 가중치에 대한 기울기 계산. 각 중간 층 $ l $에서 기울기는 다음과 같이 계산됨:
$$ \delta^l = (\delta^{l+1} \cdot W^{l+1}) \odot \sigma'(z^l) $$
여기서 $ \delta^l $ 는 층 $ l $에서의 오차, $ \delta^{l+1} $ 는 다음 층의 오차, $ W^{l+1} $는 다음 층의 가중치 행렬, $ \odot $ 는 요소별 곱(element-wise product).
5. 가중치 업데이트:
- 각 층의 가중치와 바이어스를 기울기와 학습률 $ \eta $를 사용하여 업데이트함:
$$ W := W - \eta \frac{\partial L}{\partial W} $$
$$b := b - \eta \frac{\partial L}{\partial b} $$
이 과정을 모든 데이터에 대해 반복하여 가중치와 바이어스를 점진적으로 조정함으로써 모델의 성능을 향상시킴.
딥러닝 프레임워크는 이 복잡한 과정을 자동으로 처리해주기 때문에, 상대적으로 쉽게 모델을 학습할 수 있음.
앞 선 backpropagation 과정을 코드로 표현하면,
(예제는 2층 신경망(1개의 은닉층과 1개의 출력층)으로 구성, 활성화 함수로 시그모이드 함수를 사용하고, 손실 함수로 평균 제곱 오차(MSE)를 사용함)
* backward 함수의 가중치와 바이어스 업데이트 부분 중점적으로 보기!
import numpy as np
# 활성화 함수(sigmmoid)와 그 미분 도함수
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
# 손실 함수(MSE)와 그 미분 도함수
def mean_squared_error(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
def mean_squared_error_derivative(y_true, y_pred):
return y_pred - y_true
# 신경망 클래스 정의
class SimpleNeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
# 가중치와 바이어스 초기화
self.weights_input_hidden = np.random.randn(input_size, hidden_size)
self.bias_hidden = np.zeros((1, hidden_size))
self.weights_hidden_output = np.random.randn(hidden_size, output_size)
self.bias_output = np.zeros((1, output_size))
def forward(self, X):
# 전방 전달 (forward propagation)
self.hidden_input = np.dot(X, self.weights_input_hidden) + self.bias_hidden
self.hidden_output = sigmoid(self.hidden_input)
self.output_input = np.dot(self.hidden_output, self.weights_hidden_output) + self.bias_output
self.output = sigmoid(self.output_input)
return self.output
def backward(self, X, y, output):
# 출력층의 오차 계산
error = mean_squared_error_derivative(y, output)
d_output = error * sigmoid_derivative(output)
# 은닉층의 오차 계산
error_hidden = d_output.dot(self.weights_hidden_output.T)
d_hidden = error_hidden * sigmoid_derivative(self.hidden_output)
# 가중치와 바이어스 업데이트
self.weights_hidden_output -= self.hidden_output.T.dot(d_output) * learning_rate
self.bias_output -= np.sum(d_output, axis=0, keepdims=True) * learning_rate
self.weights_input_hidden -= X.T.dot(d_hidden) * learning_rate
self.bias_hidden -= np.sum(d_hidden, axis=0, keepdims=True) * learning_rate
def train(self, X, y, epochs, learning_rate):
for epoch in range(epochs):
output = self.forward(X)
self.backward(X, y, output)
if epoch % 100 == 0:
loss = mean_squared_error(y, output)
print(f'Epoch {epoch}, Loss: {loss}')
# 데이터 생성 (예: XOR 게이트)
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
# 신경망 초기화
input_size = 2
hidden_size = 2
output_size = 1
learning_rate = 0.1
epochs = 10000
nn = SimpleNeuralNetwork(input_size, hidden_size, output_size)
# 신경망 학습
nn.train(X, y, epochs, learning_rate)
# 예측 결과 출력
print("Predictions:")
print(nn.forward(X))
'🤖 AI > Deep Learning' 카테고리의 다른 글
| [딥러닝] 6. 딥러닝 모델 학습의 문제점 pt.3 : 과적합 (1) | 2024.06.22 |
|---|---|
| [딥러닝] 5. 딥러닝 모델 학습의 문제점 pt.2 : 기울기 소실, 가중치 초기화 방법 (2) | 2024.06.12 |
| [딥러닝] 4. 딥러닝 모델 학습의 문제점 pt.1 : 최적화 알고리즘 (0) | 2024.06.10 |
| [딥러닝] 3. 딥러닝 모델 구현 (선형 회귀, 비선형 회귀 모델 구현) (0) | 2024.06.08 |
| [딥러닝] 1. Perceptron (1) | 2024.06.05 |




