[딥러닝] 1. Perceptron

 

9월 석사 입학 전 까지 목표가 있다.

딥러닝 논문을 보고, 논문을 재현(reproduction) 할 수 있을 만큼 코딩실력을 키우는 것이다.

그동안은 이론 책, 수학책을 보고 수식에 더 익숙해져 있다는 느낌을 받았는데, 이제는 코딩 능력도 키우는 것이 여름 방학 동안의 목표이다.

---

 

 

 

딥러닝 : 인공신경망에 기반하여 컴퓨터에게 사람의 사고방식을 가르치는 방법

인공신경망의 특징 : 모델 스스로 데이터의 특성을 학습하여 지도 학습, 비지도 학습 모두 적용 가능

 

 

 

1. 퍼셉트론 : 초기 형태의 신경망

 

 

 

2. 활성화 함수 : 각 뉴런의 출력 신호를 결정

• 입력 신호를 받아들여 비선형 변환 수행, 변환된 출력을 다음 층으로 전달.
• 활성화 함수는 신경망의 학습 능력과 성능에 큰 영향을 줌.

 

활성화 함수의 역할 : 

 

• 비선형성 부여: 활성화 함수는 신경망에 비선형성을 부여하여 복잡한 데이터 패턴 학습 가능. 비선형성이 없다면, 신경망은 단순한 선형 변환만 수행하게 되어 다층 구조의 의미가 없어짐.
• 신경망의 출력 범위 제한: 활성화 함수는 출력값을 특정 범위로 제한하여 안정적인 학습을 도와줌.
• 경사 하강법을 통한 학습 가능: 활성화 함수는 미분 가능해야 하며, 역전파(Backpropagation)를 통해 기울기를 계산할 수 있음.

 

주로, 시그모이드 함수(Sigmoid Function), 렐루 함수(ReLU, Rectified Linear Unit), 리키 렐루 함수(Leaky ReLU), 소프트맥스 함수(Softmax Function) 등이 활성화 함수로 사용됨

 

 

활성화 함수 선택 기준 : 각각의 활성화 함수마다 장,단점이 있으므로 실험을 통해 각 문제에 적합한 활성화 함수 선택해야 함

• 문제의 특성: 분류 문제의 출력층에서는 소프트맥스 함수를, 회귀 문제의 출력층에서는 선형 활성화 함수를 사용.
• 기울기 소실 문제: ReLU나 Leaky ReLU와 같은 함수는 기울기 소실 문제를 완화.

 

 

3. 퍼셉트론 선형 분류기

 

3.1 단층 퍼셉트론 (single layer perceptron)

단층 퍼셉트론 (single layer perceptron)

• [ 퍼셉트론 > 인공신경망 > 인공지능 ] : 퍼셉트론은 인공신경망의 논리회로 역할을 수행함
• 선형 분류를 위한 퍼셉트론 : 단층 퍼셉트론 (single layer perceptron) [예, AND, OR, NAND, NOR gate ] 

책 : 밑바닥부터 시작하는 딥러닝

 

 

[ AND gate 퍼셉트론 구현 ]

def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.7
    tmp = np.sum(x*w) + b
    if tmp <= 0:
        return 0
    else:
        return 1
    
print(AND(0,0)) # 0
print(AND(0,1)) # 0
print(AND(1,0)) # 0
print(AND(1,1)) # 1

 

 

[ NAND gate 퍼셉트론 구현 ]

def NAND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([-0.5,-0.5])
    b = 0.7
    tmp = np.sum(x*w) + b
    if tmp <= 0:
        return 0
    else:
        return 1
    
print(NAND(0,0)) # 1
print(NAND(0,1)) # 1
print(NAND(1,0)) # 1
print(NAND(1,1)) # 0

 

 

[ OR gate 퍼셉트론 구현 ]

def OR(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.2
    tmp = np.sum(x*w) + b
    if tmp <= 0:
        return 0
    else:
        return 1
    
print(OR(0,0)) # 0
print(OR(0,1)) # 1
print(OR(1,0)) # 1
print(OR(1,1)) # 1

 

 

 

3.2 다층 퍼셉트론 (MLP, multi layer perceptron)

다층 퍼셉트론 (MLP, multi-layer perceptron)

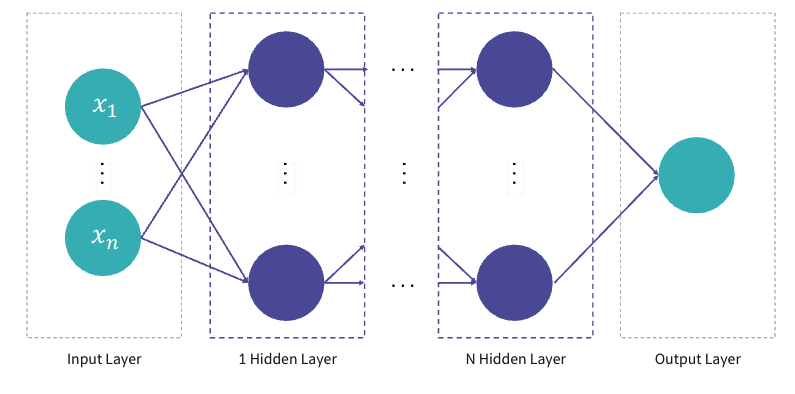
• 하나의 선(단층 퍼셉트론)으로 분류할 수 없는 문제 등장 👉 층을 쌓아 다층 퍼셉트론(multi-layer perceptron)으로 분류
• 단층 퍼셉트론을 여러층으로 쌓아 다층 퍼셉트론 형성

 

• 비선형적 논리 게이트 : XOR gate (배타적 논리합이라는 논리회로 , 두 입력값중 한쪽이 1 일때만 1을 출력)

 

• AND, NAND, OR게이트를 조합하여 XOR 게이트 생성할 수 있음.

• hidden layer : 입력층과 출력층 사이의 모든 layer
• hidden layer가 3층 이상일 경우, 깊은 신경망이라는 의미의 deep learning 사용

 

[ XOR gate 퍼셉트론 구현 : 앞서 정의한 함수 AND, NAND, OR를 쌓아서 구현 ]

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    
    return y

print(XOR(0,0)) # 0
print(XOR(1,0)) # 1
print(XOR(0,1)) # 1
print(XOR(1,1)) # 0

 

 

---

📚 Reference

• Deep Learning from Scratch 

https://search.shopping.naver.com/book/catalog/32486532054?cat_id=50010921&frm=PBOKMOD&query=%EB%B0%91%EB%B0%94%EB%8B%A5%EB%B6%80%ED%84%B0+%EC%8B%9C%EC%9E%91%ED%95%98%EB%8A%94+%EB%94%A5%EB%9F%AC%EB%8B%9D&NaPm=ct%3Dlx1t69yw%7Cci%3D84c0fa976683484f928b8ee208841cf7b90d2fb3%7Ctr%3Dboknx%7Csn%3D95694%7Chk%3D0f9e78a9f597c02602d430aaf814fd648b987612