| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 교환학생
- electrochemical models
- set method
- fluent python
- 오스트리아
- cost function
- 이차전지
- 나의23살
- Andrew ng
- anaconda 가상환경
- Deeplearning
- 특별 메소드
- set add
- 양극재
- 미래에셋해외교환
- 2022년
- 딥러닝
- fatigue fracture
- Machine learning
- Linear Regression
- special method
- li-ion
- 청춘 화이팅
- gradient descent
- 미래에셋 장학생
- 유럽 교환학생
- 선형회귀
- 유럽
- m1 anaconda 설치
- Python
- Today
- Total
Done is Better Than Perfect
[ Paper Review ] Electrochemical–mechanical coupled model for computationally efficient prediction of long-term capacity fade of lithium-ion batteries 본문
[ Paper Review ] Electrochemical–mechanical coupled model for computationally efficient prediction of long-term capacity fade of lithium-ion batteries
jimingee 2025. 2. 9. 02:50🔗 Electrochemical–mechanical coupled model for computationally efficient prediction of long-term capacity fade of lithium-ion batteries
- Journal : Journal of Energy Storage ‘24 (IF 8.9)
[ summary ]
- 제안 모델 : ISIF model, SVD-ISIF model
- Aging에 영향을 주는 mechanical fatigue fracture of cathode particles 모델링
- ISIF ( inhomogeneous stress-induced fracture)
- Electrochemical–mechanical coupled capacity fade model
- Knee point 포함한 long-term capacity degradation 예측 가능
- Electrochemical-based model과 다르게 time-consuming calculation 필요 없음
- SVD-ISIF : (hybrid model) ISIF model + Sparse variational dropout Bayesian neural network (SVDBNN)
- Long-term capacity fading data (3000 to 20,000 cycles)의 실험 데이터로 검증
1. Problem Statement
[ Existing method ]
1. Electrochemical model
- Strength : Reflect various physical phenomena using physical parameters and principles
- Weakness : Cannot be generalization, Difficult to solve quickly
- It composed of many physical parameters & complex coupled nonlinear PDE
2. Empirical model
: Designed to reflect empirically obtained key features of capacity fade trends
- Strength : Small number of parameters & simple equations
- Weakness : Too simple to reflect the effects of capacity fade patterns (e.g. knee point)
3. Data-driven capacity model
- Strength : Capture complex aging dynamics through implicit analysis of data
- Weakness : Inability to predict the entire lifespan, Require large amounts of data
[ Proposed method ]
1. ISIF (Inhomogeneous stress induced fracture) model
- Electrochemical–mechanical coupled capacity-fade model
- Model mechanical fatigue fracture of cathode particles
- Predict long-term capacity-fade including knee-point
2. SVD-ISIF model (hybrid model)
- (SVDBNN) Sparse Variational Dropout Bayesian neural network → data-driven model
- Improve accuracy & data efficiency, especially when data is abundant
2. Contribution
- Ability to predict the capacity fade over the entire battery lifespan, long-term (3000 to 20,000 cycle) capacity fade including the ‘‘knee point’’
- Ability to predict the capacity fade using only the operating conditions, without early cycle experimental data
- Smaller computational burden and fewer model parameters than electrochemical models
3. Methodology
Total capacity fade = capacity fade in cathode + capacity fade in anode
- In cathode, Fatigue fracture of cathode particles → LAM (Loss of Active Material)
- In anode, SEI layer formation, lithium plating on the surface of the anode particles → LLI (Loss of Lithium Inventory)
In this paper, express ‘Amount of capacity fade’ using ‘RCL (relative capacity loss)’
(2) Total RCL (n-th aging cycle) = RCL by cathode degradation + anode degradation

[ ISIF model scheme ]
- Input : Aging cycle condition & the number of aging cycles (N)
- Output : RCL
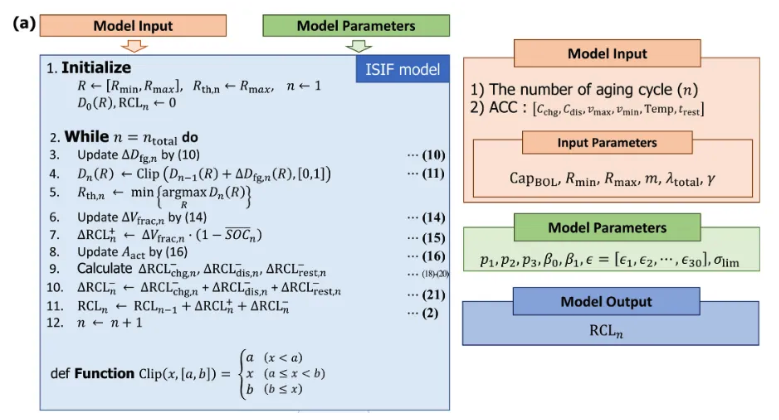
3.1 Capacity fade caused by cathode degradation ( $\Delta RCL_n^+$ )
: In cathode, Fatigue fracture of cathode particles → lead LAM (Loss of Active Material)
: Fatigue fracture is the result of cyclic stress (due to lithium intercalation / deintercalation)
3.1.1 Fatigue fracture in solid materials
- (3) S-N curve equation
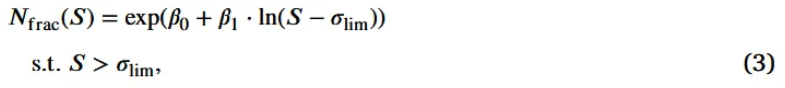
- (4) Fatigue damage fraction

- (5) Cumulative damage (from 1 to n-th aging cycle)
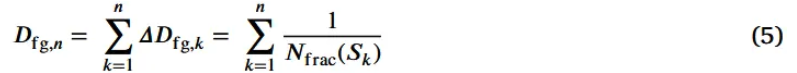
3.1.2 Fatigue damage of individual cathode particles
- (6) Surface tangential stress (at time t with radius R) on cathode particles

- (7) Maximum tangential stress that causes crack generation (set $ k_s^+$ as variable)

- (8) Define function $ f(C_{chg,n})$ that fits 2-dimensional polynomial of $ C_{chg,n} $
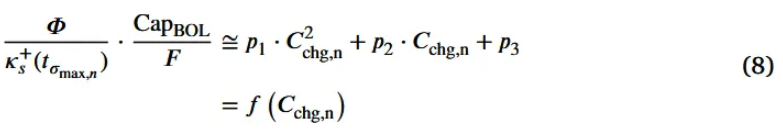
- (9) Update stress range applied to the particle of radius R at the n-th aging cycle
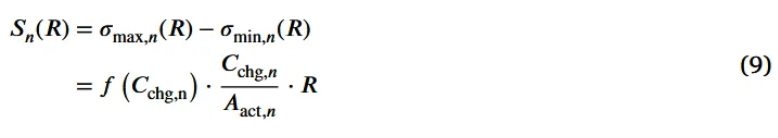
- (10) Update fatigue damage fraction for radius R particle due to the n-th single aging cycle

- (11) Update Cumulative damage during aging cycle

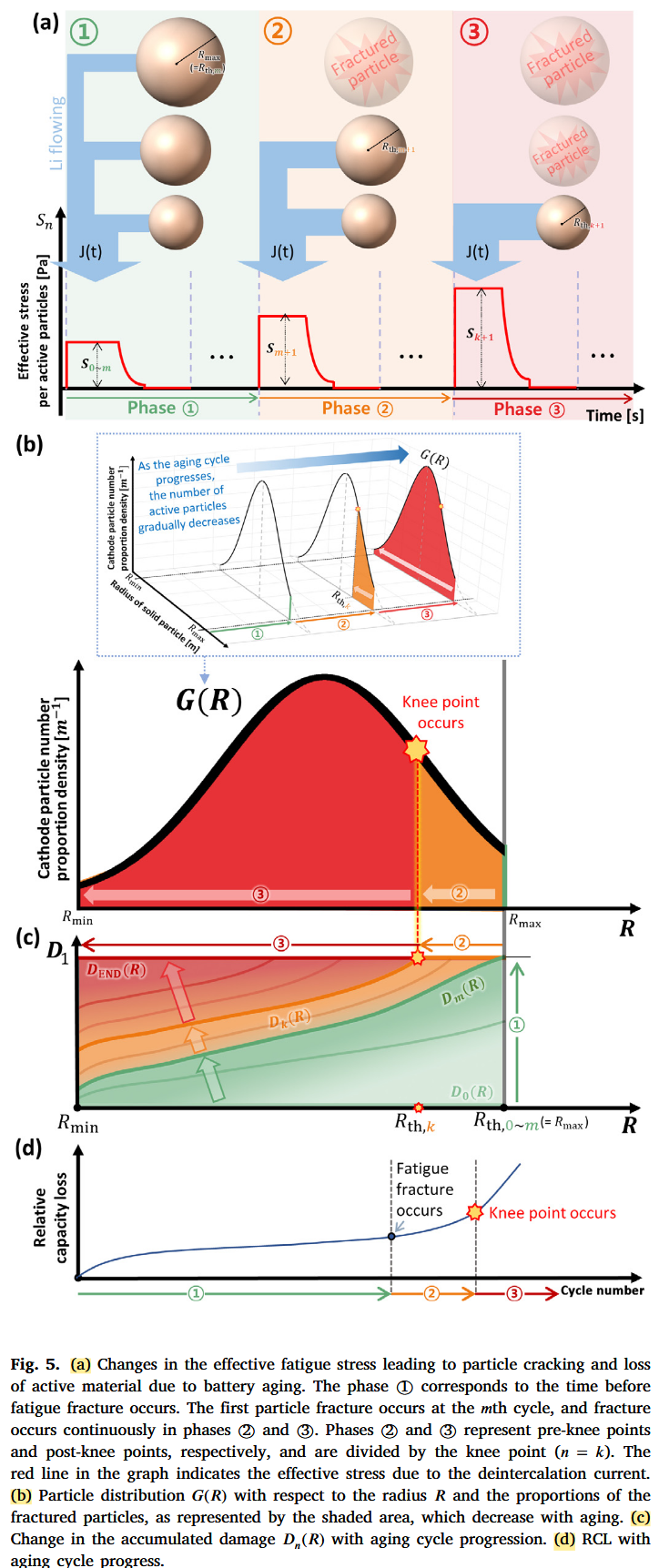
3.1.3 Fatigue fracture of entire cathode particles
1️⃣ time before fatigue fracture / 2️⃣ pre-knee point / 3️⃣ post-knee point / knee point (n=k)
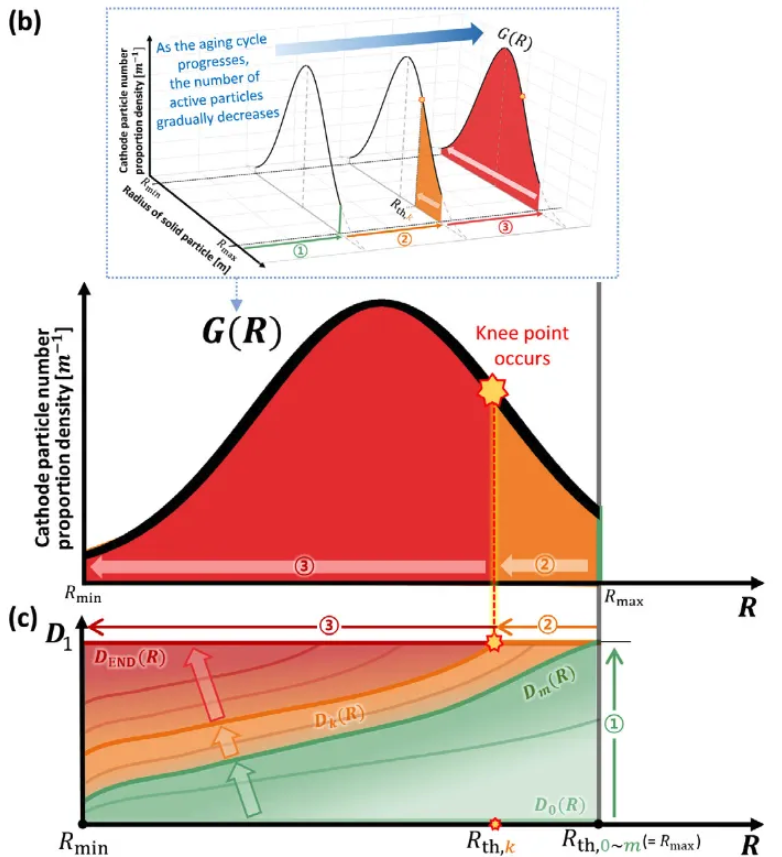

- Assume : radius R of cathode particles within range $[R_{min}, R_{max}]$ (Fig.5 (b)
- The larger electrode particles suffer from more fatigue damage → $D_n(R)$ is monotonically increasing function (Eq.11)
- $D_n(R)$ lead to the update of $R_{th,n}$(the smallest fractured cathode particle in the n-th aging cycle)
- (12) Particle number distribution & (13) Normal distribution of particle number according R

3.1.4 Capacity loss due to cathode degradation
- (14) Reduced proportion of room for storing lithium in cathode particles
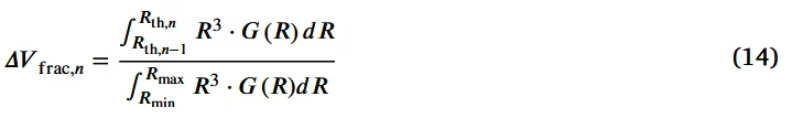
- (15) RCL caused by cathode degradation

- (16) Total active surface area of the cathode particles
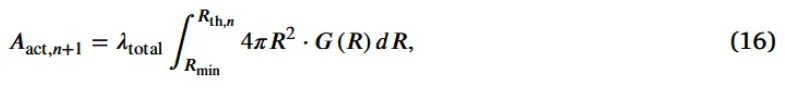
As aging : With decrease $R_{th,n}$ → decrease $A_{act, n+1}$ → increase $S_n(R)$ in Fig.5
- $R_{th,n}$ : n-th cycle에서 cathode particle Radius
- $A_{act, n+1}$ : n+1 cycle에서 active particle의 Area
- $S_n(R)$ : n-th cycle에서 cyclic stress range (S)
3.2 Capacity fade caused by anode degradtion ( $\Delta RCL_n^-$ )
: In anode, SEI layer formation, lithium plating on the surface of the anode particles
- (17) Aging density function

- Change in RCL during (18) charging, (19) discharging, (20) rest

- (21) Total change in the RCL due to anode degradation in the n-th aging cycle
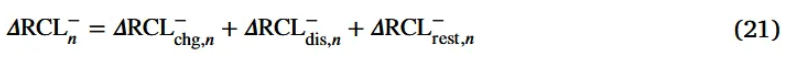
3.3 SVD-ISIF model : A hybrid capacity fade model
Hybrid model : ISIF + Sparse Variational Dropout Bayesian Neural Network (SVD)
- Improve accuracy
- Provide uncertainty of the prediction
Sparse Variational Dropout Bayesian Neural Network (SVDBNN)
- Strength : better generalization performance than traditional Bayesian Neural Networks (BNNs) due to its sparser network structure
- Network size : 6-400-300-1
- Batch size : 200 / Epoch of learning : 10
[ SVD-ISIF model scheme ]
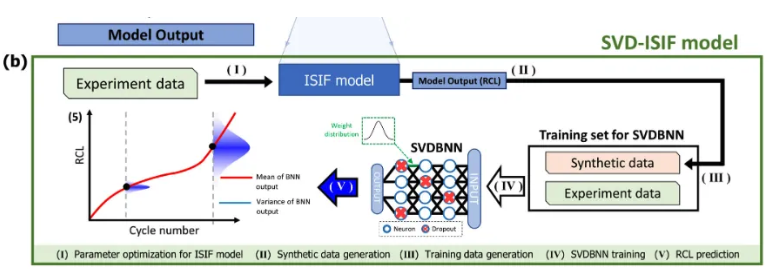
- Input : Aging cycle condition & the number of aging cycles (N)
- Output : RCL & uncertainty of the prediction result
4. Experiment Result Anaylsis
[ Experimental Setup ]
- Long-term (>3000 cycles) experimental data of 2170 NCM batteries
- 25 ◦C inside a constant temperature and humidity chamber
- Use RCL (relative capacity loss) to express capacity fade
- Profile : 20 types of different aging cycle (CCCV)
- Cycle (#8-9. #18-20) has knee points (Fig. 2)
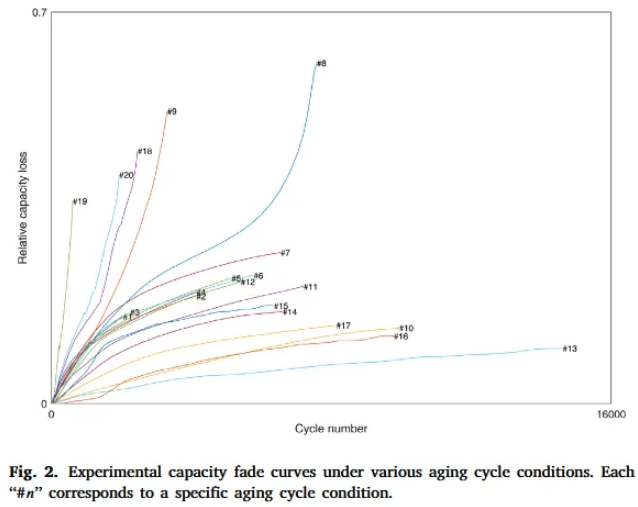
- Configuration of Profile
: Consisted of repeated aging cycles and periodic reference performace tests (RPTs)
- RPTs: To measure capacity periodically
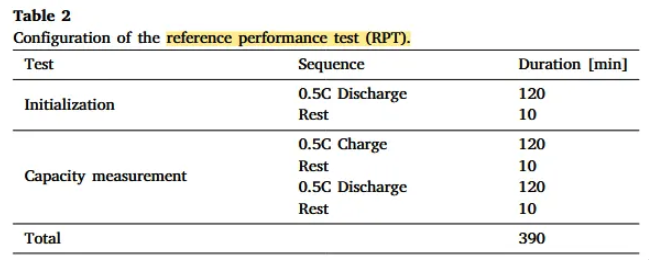
- Aging cycle test (single cycle )
- charging in constant current(CC)–constant voltage(CV) mode
- 10-min rest
- discharging in CC mode
- 10-min rest
[ Result Analysis ]
1. Computational Time
- #12 aging cycle condition, which had a total length of 14,613 cycle
- Compare simulation time
- P2D+SEI : P2D model incorporating capacity fade due to SEI layer formation
- P2D (SEI+CRACK) : P2D model incorporating capacity fade due to SEI layer formation and particle cracking
- ISIF model
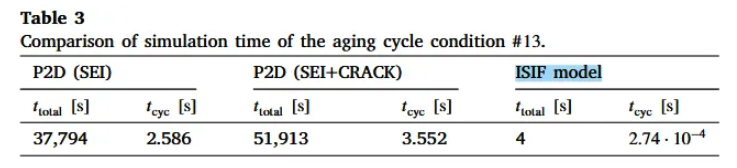
- ISIF model has a lower computational burden
- ISIF model focus on key aging mechanisms for predicting capacity fade
2. Prediction Accuracy
[ Experiment Setup ]
- K-fold cross-validation (K=20)
- Among 20 time-series experimental datasets, train dataset : 19 / test dataset : 1
- Model : ISIF model, SVDBNN, SVD-ISIF model
- Metric : MAE(Mean Average Error) & MxAE(maximum absolute error)
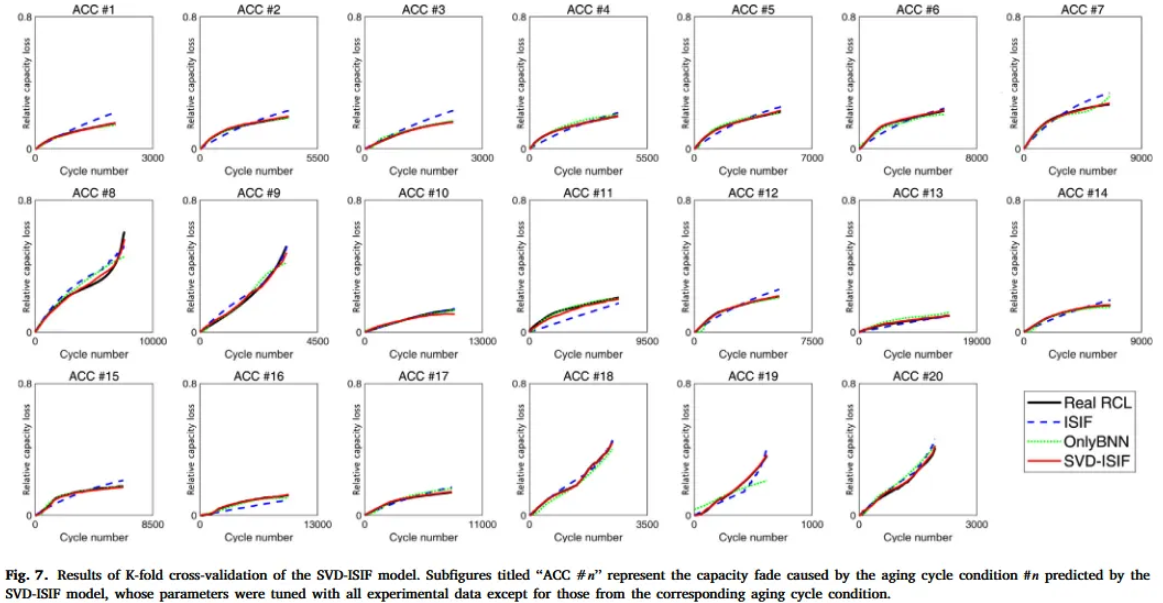
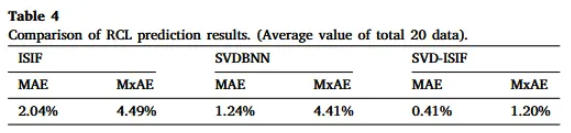
1. Comparing ISIF model and SVDBNN
- Both MAE and MxAE show similar values
- ISIF shows uniform estimation performance across all aging cycle conditions
- SVDBNN shows very low prediction accuracy for data with specific aging cycle condition or knee points → Fig. 8 ( Aging cycle condition #9, #19 )
- Only SVDBNN fails to predict the tendency of knee point → impractical to use SVDBNN
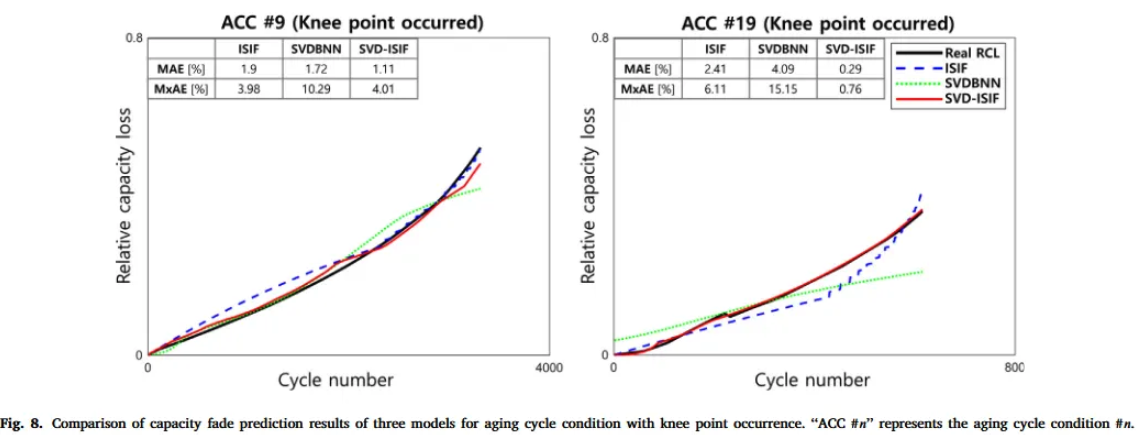
2. SVD-ISIF model
- SVD-ISIF model shows high estimation performance at both MAE, MxAE
- Demonstrate that combining ISIF and BNN can reduce overfitting
5. Conclusion
- ISIF model
- Predict long-term capacity fade with small computation burden
- Not require early cycle data → only require the aging cycle condition
| ISIF model | SVD-ISIF model |
| small computation burden | higher computation burden, better generalization |
| lower prediction accuracy | higher prediction accuracy |
Limitation
- Not reflect the effects of temperature, different cathode materials, transient particle stresses
'🔋 이차 전지 > 논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] 🤖🔌 강화학습을 사용한 열화 최소화 급속 충전 프로파일 (0) | 2025.02.23 |
|---|---|
| [ Paper Review ] Capacity Estimation Through Knowledge Transfer (5) | 2024.09.27 |
| [ Paper Review ] Strategically switching metaheuristics for effective parameter estimation (0) | 2024.09.16 |
| [ Paper Review ] Parameters for degradation diagnosis (2) | 2024.09.01 |
| [논문 리뷰] 배터리 열화의 핵심 문제 (key issue of the lithium ion battery degradation) (2) | 2024.08.22 |




